50 Work Energy Theorem Facts: Explanations, Examples

Scientific theories play a pivotal role in simplifying and organizing the complex world around us. They provide a systematic framework for understanding natural phenomena and have a profound impact on how we interact with and manipulate our environment. These theories serve as the cornerstones of scientific knowledge, guiding our exploration of the physical universe. One such fundamental concept is the Work-Energy theorem, with its interesting facts stands as a testament to the power and utility of scientific principles in our daily lives. This article will feature some interesting work-energy theorem facts. Keep reading.

The Work-Energy theorem stands as a testament to the power of scientific theories in simplifying and improving our lives. Its foundational role in physics extends its influence into diverse fields, from engineering to renewable energy and sports. By embracing and applying this fundamental principle, we continue to innovate and advance our understanding of the world, ultimately contributing to a more efficient, sustainable, and accomplished society.

Work Energy Theorem interesting Facts:

Find below some interesting facts about the work-energy theorem:

1. The Work-Energy Theorem: A Fundamental Scientific Principle

The Work-Energy theorem is an essential principle in the realm of physics, offering a profound insight into the relationship between force, work, and kinetic energy. At its core, this theorem asserts that in the absence of other forces acting on an object, the work done by an applied force is equal to the change in kinetic energy experienced by the object. This seemingly simple concept carries profound implications and has far-reaching applications across various scientific disciplines and practical domains.

2. Analytical Calculation Over Instinctual Intuition

In the realm of physics and engineering, there is a fundamental shift from relying solely on intuitive instincts to employing analytical calculations. Instead of merely pushing an object and expecting it to move at a certain speed, this shift involves the meticulous process of precisely determining the required force and the resulting velocity.

3. The Importance of Work-Energy Theorem in Machinery

In the domain of machinery and industrial operations, the work-energy theorem plays a pivotal role. It serves as the underlying principle that governs the functionality of factories and machines. Moreover, it is the reason behind the (relatively) efficient operation of these mechanical systems. This theorem is of paramount importance, as it offers a comprehensive understanding of how much work can be accomplished by these machines, thereby enabling us to make informed decisions about their use.

4. The Significance of Knowing Horsepower in Vehicles:

Understanding the concept of horsepower and its relevance is crucial, especially in the context of vehicles. The horsepower rating of an engine is a direct measure of its capability to perform work, and it is intricately linked to the work-energy theorem. By comprehending the horsepower of our vehicles, we gain insights into their ability to perform tasks and move loads efficiently. This knowledge is vital in the physical world, as it empowers us to make informed choices about the vehicles we use and their suitability for various tasks and applications.

5. Unveiling the Impact of the Work-Energy Theorem

To truly appreciate the significance of the Work-Energy theorem, it is essential to explore its applications from multiple perspectives. This article aims to shed light on the theorem’s real-world relevance by presenting examples and explanations from three distinct angles. By delving into these perspectives, we can gain a deeper understanding of how this fundamental scientific principle underpins numerous inventions and activities that shape our world.

6. Mechanical Engineering and Motion Control

The Work-Energy theorem finds extensive utility in the field of mechanical engineering, particularly in the design and analysis of mechanisms and systems involving motion. Engineers and designers leverage this theorem to optimize the performance of various machines, such as automobiles, aircraft, and industrial equipment. By understanding how work and energy are interconnected, engineers can improve efficiency, reduce energy consumption, and enhance the overall functionality of these complex systems. The Work-Energy theorem serves as a guiding principle in the development of cutting-edge technologies that propel our society forward.

7. Renewable Energy and Environmental Sustainability

In the quest for a more sustainable future, the Work-Energy theorem plays a crucial role in the realm of renewable energy. Systems like wind turbines, solar panels, and hydroelectric generators rely on the principles outlined in this theorem to harness and convert natural forces into usable energy. By optimizing the conversion of mechanical work into electrical energy, these technologies contribute to reducing our dependence on fossil fuels and mitigating the environmental impact of energy production. The Work-Energy theorem, in this context, paves the way for a greener and more eco-friendly energy landscape.

8. Sports and Human Performance

Beyond the realm of machines and environmental applications, the Work-Energy theorem also finds relevance in the world of sports and human performance. Athletes and coaches utilize this principle to maximize performance and efficiency in various sports. Understanding how to apply force to achieve optimal work and energy transfer is essential in activities like sprinting, cycling, and weightlifting. By harnessing the principles of the Work-Energy theorem, athletes can improve their techniques, set records, and push the boundaries of human physical capabilities. This application underscores the theorem’s versatility and its impact on enhancing human achievement.

9. Understanding the Impact of Gravity on Work and Kinetic Energy

When we examine the forces acting on an object, particularly in the context of gravity, we can gain valuable insights into how work and kinetic energy are interrelated. Specifically, if we isolate gravity as the sole force acting on an object, we can establish a direct correlation between the work done by gravity and the resulting change in kinetic energy. This relationship is dependent on the direction of motion: if the object is in a state of descent, the change in kinetic energy will be positive, signifying an increase, while if the object is moving upward, the change will be negative, indicating a decrease.

10. The Work-Energy Theorem

The Work-Energy Theorem is a fundamental principle in physics that formalizes the connection between work applied to a system and the resulting change in the system’s energy. In essence, it quantifies how work contributes to the transformation of energy within a system. This theorem can be expressed mathematically using the following equation:

ΔE = W

Where:

ΔE represents the change in the energy of the system.
W denotes the work done on the system.

This equation serves as a concise and powerful tool for analyzing physical systems, allowing us to predict how energy changes when work is applied. It underscores the concept that energy is a conserved quantity, and any work done on a system leads to a corresponding change in its energy state. The Work-Energy Theorem provides a foundation for understanding and solving a wide range of problems in physics, shedding light on the intricate relationship between work and energy. Buy Electronic Components, lC chips, Module Darlington, Capacitor, find chips, diode, Transistors, Sensors, and IGBT at Utsource.

11. The Work-Energy Theorem: A Comprehensive Explanation

In the realm of physics, the Work-Energy Theorem is a fundamental concept that sheds light on the relationship between work, force, and energy. This theorem plays a pivotal role in understanding the behavior of physical systems and is applicable in various contexts. This article aims to delve deeper into the Work-Energy Theorem, breaking down its key components and elucidating its significance in the world of science.

Work as the Net Force Along a Path

First and foremost, let’s clarify a common misconception. While many individuals equate work to the formula W = pressure x distance, the concept of work in physics is more nuanced. Correctly defined, work is the net force acting on a system integrated along its path of motion. This distinction is crucial for a comprehensive understanding of the Work-Energy Theorem.

Conservation of Energy

One of the bedrock principles in physics is the conservation of energy. It asserts that energy cannot be created or destroyed but can only change forms. When an external force performs work on a system, the Work-Energy Theorem proclaims that this work doesn’t vanish into thin air; instead, it contributes to the system’s total energy.

Classifying Energy Effects

To keep track of this energy, physicists classify its effects into several categories. Firstly, it can manifest as the kinetic energy of the system, representing the energy of motion. Secondly, energy can be stored in the system in various forms, constituting potential energy. Lastly, it can be randomly distributed within the system’s atoms, resulting in heat energy, among other possibilities. Understanding these classifications is pivotal in practical applications.

The Work-Energy Theorem in a Nutshell

In essence, the Work-Energy Theorem establishes a crucial link between the concept of work, defined as force multiplied by displacement, and the notion of energy, encompassing kinetic and potential energy. This connection is immensely valuable across numerous scientific disciplines and real-world scenarios.

12. Dynamic Role in Physics

The Work-Energy Theorem is not a mere theoretical construct; it plays a dynamic and central role in the field of physics. This theorem bridges the gap between work, a vector quantity, and energy, a scalar quantity, allowing them to be treated together. It elegantly states that the change in the kinetic energy of a system is equal to the work done on the system.

Illustrative Example

Imagine you are roller skating and want to determine the amount of friction acting on your wheels. As you start skating and accelerate to, say, 10 mph, eventually, you will decelerate due to friction. Let’s assume you end up traveling at 5 mph. You can calculate the change in your kinetic energy, provided you know your mass.

This change in kinetic energy is equated to the work performed by friction to slow you down—a testament to the Work-Energy Theorem’s applicability. Since work equals the force exerted multiplied by the distance over which it’s exerted, knowing both the total work (change in kinetic energy) and the distance (e.g., 100 feet) allows you to calculate the average force exerted by friction.

Conservation of Energy in Action

At its core, the Work-Energy Theorem underscores the principle of energy conservation. Any alteration in the energy of a system, such as your deceleration on skates, must be accounted for. This theorem specifically states that this change in the kinetic energy of a system equals the work done on the system by external forces, as demonstrated in the example involving friction.

Fundamentals for Understanding Our Material World

The Work-Energy Theorem provides a foundational framework for comprehending the mechanics of our material world. It reveals the intricate interplay between force, work, and energy, serving as a cornerstone in physics and countless applications. Understanding this theorem is essential for scientists and anyone intrigued by the fundamental workings of the physical universe.

13. Understanding the Work-Energy Theorem

Physics can often be a perplexing field, filled with complex mathematical and conceptual challenges. One of these challenges arises when dealing with vectors and their trigonometric breakdowns, particularly in problems related to energy. However, there is a valuable concept that simplifies these issues significantly—the work-energy theorem.

The Scalar Nature of Energy

The work-energy theorem’s potency lies in the fact that energy is a scalar quantity. Unlike vectors, which have both magnitude and direction, scalars only possess magnitude, making them far more manageable in calculations. This inherent simplicity in dealing with scalar energy values is what makes the work-energy theorem a valuable tool for physicists and engineers alike.

An Escape from Trigonometric Vector Breakdowns

For those who have struggled with the complexities of trigonometric vector breakdowns in physics problems, the work-energy theorem offers a respite. It’s a tool that can rescue you from the frustrations of dealing with vectors, provided you understand its principles and limitations.

Not a Universal Solution

While the work-energy theorem can be a lifesaver in many physics scenarios, it’s essential to acknowledge its limitations. Not all problems can be effectively tackled using the concept of energy. In certain situations, more specialized principles and equations may be required to reach a complete solution.

The Golden Ticket of Physics

Consider the work-energy theorem as a golden ticket within the realm of physics. It often acts as a magic key that can unlock the solutions to a wide range of problems. When wielded correctly, it can guide you precisely to the answers you seek in your physics endeavors.

Unifying Different Forms of Energy

One aspect of the work-energy theorem that might initially appear counterintuitive is its ability to connect various types of energy—such as kinetic, potential, and elastic—to the work done by external forces or factors like friction. This might seem perplexing at first, but the beauty of this equation lies in its adaptability. It allows you to select the relevant terms based on the specific scenario you are dealing with, ultimately leading you toward a solution.

14. The Work-Energy Relationship

At its core, the work-energy theorem establishes a fundamental relationship between work and energy. According to this theorem, the kinetic energy of an object is equal to the work required to accelerate it to a certain velocity. In simpler terms, the kinetic energy (KE) of an object is directly related to the amount of work done on it to attain a specific speed.

Determining Work and Energy

With an understanding of the kinetic energy equation, KE = ½ mv², you can now calculate the amount of work needed to bring an object to a particular velocity. Additionally, knowing the kinetic energy also equips you with the knowledge of the work required to bring the object to a complete stop.

The Work Required for Velocity Changes

For an object with mass ‘m’ and velocity ‘v’, the equation KE = ½ mv² = W = Fd = mad simplifies the work-energy relationship. It tells us that the work required to change an object’s velocity from rest to ‘v’ or from ‘v’ to rest is equal to the object’s kinetic energy. This simple yet powerful relationship bridges the gap between work and energy, offering a valuable tool for solving a wide range of physics problems.

15. Work Energy Theorem Proof

Introduction: The Work-Energy Theorem is a fundamental concept in physics that relates the work done on an object to the change in its kinetic energy. It provides a powerful tool for analyzing the motion of objects subjected to various forces.

Derivation: The proof of the Work-Energy Theorem begins by considering the work done on an object by a constant force. For a constant force F acting along a straight path, the work W done is given by the formula W = F * d * cos(θ), where F is the force, d is the displacement, and θ is the angle between the force and the displacement vectors. Integrating this expression over the entire path yields the work done.

Kinetic Energy: Next, we introduce the concept of kinetic energy (KE) as 1/2 * m * v^2, where m is the mass of the object and v is its velocity. The change in kinetic energy, ΔKE, is equal to the final kinetic energy minus the initial kinetic energy.

Putting It All Together: By equating the work done on the object to the change in kinetic energy, we arrive at the Work-Energy Theorem: W = ΔKE. This theorem applies not only to objects subjected to constant forces but also to those experiencing variable forces as long as the work done by those forces can be calculated.

16. Work Energy Theorem Formula

Formula: The Work-Energy Theorem is expressed by the formula: W = ΔKE. In this equation, W represents the work done on an object, and ΔKE represents the change in kinetic energy of the object.

Interpretation: This formula underscores the fundamental relationship between work and energy in the context of an object’s motion. It states that the work done on an object is equal to the change in its kinetic energy. If the work is positive, it increases the object’s kinetic energy, whereas negative work decreases it.

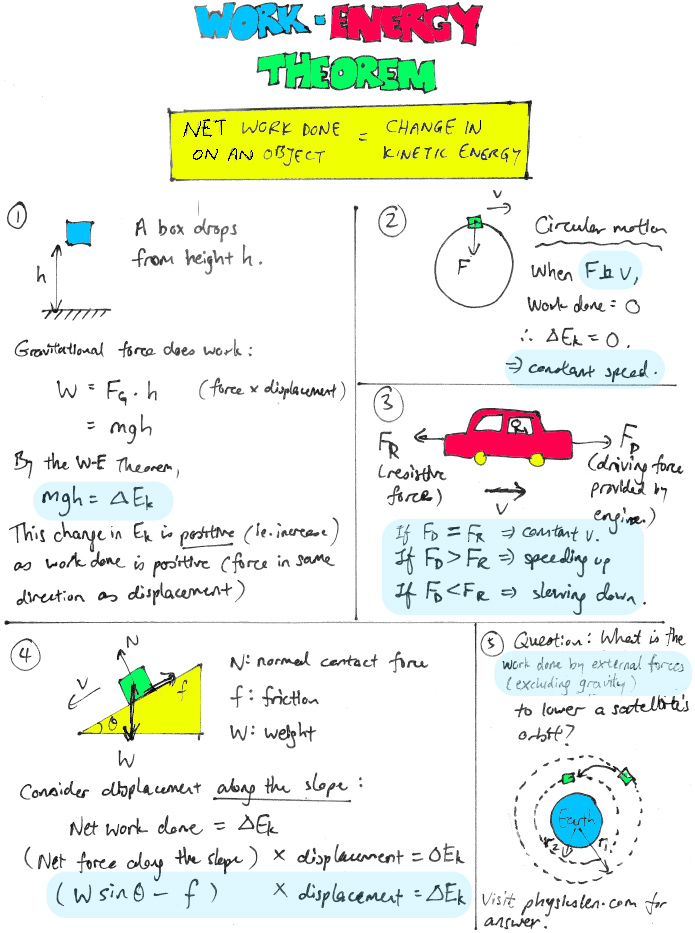
17. Work Energy Theorem Equation

Equation: The Work-Energy Theorem can be written in equation form as follows: W = ΔKE. Here, “W” represents the work done on an object, and “ΔKE” stands for the change in the object’s kinetic energy.

Practical Application: This equation finds wide application in physics and engineering, particularly in situations where forces are involved. Engineers use it to analyze the motion of vehicles, machinery, and structures, while physicists employ it to understand and predict the behavior of particles and objects subjected to various forces.

18. Work Energy Theorem for Variable Force

Introduction: The Work-Energy Theorem isn’t limited to scenarios with constant forces. It can also be applied to situations involving variable forces, such as non-constant forces acting on an object.

Extension of the Theorem: In cases where the force acting on an object varies with position, time, or other parameters, the work done by this variable force can still be calculated using integration. By integrating the force over the path or time interval of interest, you can determine the total work done.

Generalization: The Work-Energy Theorem for variable forces is a generalization of the original theorem and provides a valuable tool for analyzing complex systems where forces change continuously during an object’s motion.

19. Work Energy Theorem Examples

Introduction: To gain a better understanding of the Work-Energy Theorem, it’s helpful to explore some practical examples where it can be applied.

Example 1 – Falling Object: Consider a ball dropped from a certain height. Gravity exerts a constant force on the ball. By calculating the work done by gravity as the ball falls, you can use the Work-Energy Theorem to find its final kinetic energy, which is directly related to its velocity.

Example 2 – Spring Compression: When a spring is compressed, a variable force is applied to it. By integrating this force over the distance the spring is compressed, you can determine the work done on the spring. This work is equal to the potential energy stored in the compressed spring.

Example 3 – Car Acceleration: In a car, the engine exerts a varying force to accelerate it. By calculating the work done by the engine’s force as the car accelerates, you can find the change in kinetic energy of the car, which relates to its speed.

Conclusion: These examples illustrate the versatility and applicability of the Work-Energy Theorem in analyzing real-world situations involving various forces and energy transformations. It is a fundamental principle in physics that aids in understanding and predicting the motion of objects and systems.

20. What is the Work-Energy Theorem and why is it significant in physics?

The Work-Energy Theorem is a foundational principle in the realm of physics that serves as a crucial tool for explaining and quantifying the relationship between the work exerted on an object and the resultant alteration in its mechanical energy. This theorem functions as a fundamental framework that enables physicists and scientists to gain insight into how external forces can induce changes in the overall energy content of a system.

The Work-Energy Theorem is a fundamental concept in physics that elucidates the connection between the work done on an object and the subsequent changes in its mechanical energy. It plays a pivotal role in our understanding of how external forces influence the energy dynamics of a system.

The Mathematical Formulation of the Work-Energy Theorem

The Work-Energy Theorem is succinctly articulated through a mathematical expression, which aids in quantifying the relationship between work and energy alteration. This formula is instrumental in precisely describing the interplay between these two crucial concepts.

21. What is the mathematical representation of the Work-Energy Theorem?

The Work-Energy Theorem is mathematically denoted as follows:

W=ΔKEW=ΔKE

Where:

– W represents the work done on the object.
– ΔKE signifies the change in the kinetic energy of the object.

3. Illustrative Examples of the Work-Energy Theorem

To grasp the practical applications and implications of the Work-Energy Theorem, it is beneficial to explore tangible scenarios where they come into play. Several illustrative examples shed light on how this theorem manifests in real-world situations.

22. How does the Work-Energy Theorem manifest in everyday scenarios?

The Work-Energy Theorem manifests in various scenarios, including:

a. Lifting a Weight: When an individual lifts a weight against the force of gravity, they are actively performing work on the object, consequently augmenting its potential energy.

b. Swinging a Pendulum: The motion of a pendulum is a quintessential example of the interconversion between potential and kinetic energy, as it oscillates back and forth.

c. Accelerating a Car: When a vehicle accelerates, external forces are applied to it, leading to an increase in its kinetic energy, which aligns with the principles of the Work-Energy Theorem.

The Fundamental Significance of the Work-Energy Theorem

Understanding why the Work-Energy Theorem holds a crucial place in the realm of physics is integral to appreciating its broader implications. This theorem emerges as a direct consequence of a fundamental principle in physics, the conservation of energy, and serves to elucidate how energy is transferred and transformed within a system when subjected to external forces.

23. What is the Work-Energy Theorem and Its Applications?

The Work-Energy Theorem is a fundamental principle in physics that finds wide-ranging applications in various branches of the field, including mechanics, thermodynamics, and electromagnetism. This theorem serves as a powerful tool for understanding the relationships between work and energy in physical systems. Its applications are diverse and include tasks such as analyzing the motion of objects subjected to various forces, calculating the efficiency of machines, and gaining insights into the behavior of subatomic particles in particle accelerators.

24. What is the Work-Energy Theorem in Joules?

The Work-Energy Theorem is conventionally expressed in joules (J), which is the standard unit of energy in the International System of Units (SI). When the Work-Energy Theorem is applied, it quantifies the transfer of energy in terms of joules when work is performed on an object. This allows for a consistent and measurable representation of energy transformations.

25. Is the Work-Energy Theorem True?

A: Yes, the Work-Energy Theorem is a well-established and experimentally verified principle in physics. It has been extensively tested and consistently upheld in various physical systems. This theorem accurately describes the connection between the work done on an object and the resulting changes in its energy, making it a fundamental and reliable concept in the field of physics.

26. Is the Work-Energy Theorem Universal?

The Work-Energy Theorem is considered a universal principle within classical mechanics, and it is applicable to a wide range of physical phenomena encountered in everyday situations. However, it may not hold true in extreme conditions, such as those involving relativistic speeds or quantum mechanics, where classical mechanics no longer accurately describes physical phenomena. Nonetheless, within its domain of applicability, the Work-Energy Theorem is a versatile and essential tool.

27. How is the Work-Energy Theorem Used in Real Life?

The Work-Energy Theorem finds extensive application in diverse real-life situations, offering valuable insights and aiding in the optimization of processes. Here are some detailed examples:

Designing Efficient Engines: Engineers utilize the Work-Energy Theorem to design efficient combustion engines. By understanding how the work done on the fuel-air mixture translates into kinetic energy, they can optimize the engine’s performance, improving fuel efficiency and reducing emissions.

Analyzing Vehicle Motion: When analyzing the motion of vehicles, such as cars, airplanes, or rockets, the theorem plays a crucial role. It helps engineers determine the energy required for propulsion and the work done against friction and air resistance, which is essential for designing fuel-efficient transportation systems.

Calculating Energy Consumption: In everyday life, we use the Work-Energy Theorem when calculating the energy consumption of appliances. By measuring the work done to operate these devices, such as refrigerators, air conditioners, or washing machines, we can estimate their energy consumption and make informed decisions about energy conservation.

Understanding Projectile Motion: Physicists and engineers apply the theorem to understand the behavior of projectiles like missiles or baseballs. By considering the work done by gravity and air resistance, they can predict the trajectory and speed of projectiles, aiding in military applications, sports, and space exploration.

28. Is the Work-Energy Theorem Applicable Everywhere?

The Work-Energy Theorem is a fundamental concept in classical mechanics and boasts wide applicability within this realm. However, it does have limitations, particularly when dealing with phenomena at the quantum or relativistic scales. Let’s delve into this in more detail:

Classical Mechanics: The Work-Energy Theorem is perfectly applicable to classical mechanical systems, which encompass the motion of everyday objects, machinery, and celestial bodies like planets and stars. It is the cornerstone of classical physics.

Quantum Mechanics: At the quantum level, where particles exhibit wave-particle duality and behaviors that defy classical intuition, the Work-Energy Theorem loses its straightforward applicability. Quantum mechanics relies on different principles, such as wavefunctions and probability distributions, to describe particle behavior.

Relativistic Physics: In the realm of relativistic physics, where objects approach the speed of light, classical mechanics breaks down, and the Work-Energy Theorem becomes less accurate. Einstein’s theory of relativity takes precedence in these scenarios, providing a more comprehensive framework.

In essence, while the Work-Energy Theorem remains a powerful tool for understanding and solving problems in classical mechanics, it may not provide accurate predictions or descriptions in the complex and exotic domains of quantum mechanics and relativistic physics.

29. Is the Work-Energy Theorem Valid Only for Particles?

The Work-Energy Theorem is not constrained to particles alone; it can be successfully applied to systems of particles and even continuous objects, as long as the fundamental principles of mechanics apply. Let’s explore this concept further:

Individual Particles: The theorem certainly applies to single particles, helping us understand how their kinetic and potential energy change as work is done on them or by them.

Systems of Particles: When dealing with systems of particles, such as a group of interconnected objects or a collection of particles in a rigid body, the Work-Energy Theorem is still valid. It allows us to analyze the overall energy changes in the system as a result of external forces and internal interactions.

Continuous Objects: Even for continuous objects, like a rotating wheel or a stretching rubber band, the Work-Energy Theorem holds true. By dividing these objects into infinitesimal elements and considering their collective behavior, we can use the theorem to understand how energy is transferred and transformed within them.

In summary, the Work-Energy Theorem offers a versatile framework for analyzing energy changes in a wide range of mechanical systems, whether they involve single particles, multiple particles, or continuous objects.

30. When Can the Work-Energy Theorem Be Used?

The Work-Energy Theorem can be effectively utilized whenever specific conditions are met, facilitating a comprehensive understanding of energy transformations within a system. Here’s a more detailed explanation:

Presence of External Forces: The theorem is applicable when external forces are at play, either doing work on an object or receiving work from the object. These forces can be gravitational, frictional, electrical, or any other form of external influence.

Work Being Done: For the Work-Energy Theorem to be useful, work must be involved. Work is defined as the product of force and displacement in the direction of the force. The theorem helps quantify how this work changes the energy of the system.

Energy Transformation: The theorem is employed to assess how energy is transformed within a system. It allows us to track the conversion between potential and kinetic energy or other forms of energy, providing valuable insights into the system’s behavior.

In essence, the Work-Energy Theorem is a powerful tool in mechanics, aiding in the analysis of energy changes whenever there is a clear interplay of external forces and the transfer of work within a system.

31. What Does It Mean When Work Is Positive?

When work is designated as positive, it carries a specific meaning in the context of the Work-Energy Theorem, and it often arises in certain situations. Let’s delve into this concept in more detail:

Energy Transfer: Positive work indicates that energy is being transferred to the object, leading to an increase in its energy state. This occurs when an external force is applied in the direction of the object’s motion.

Direction of Force: The direction of the force applied aligns with the direction of displacement. In other words, the force aids the object in moving in the same direction in which the force is exerted.

Examples: Positive work is commonly observed when lifting an object against gravity, pushing a car forward, or accelerating an object by applying a force in the direction of motion. In each case, the energy of the object increases due to the work done on it.

In summary, when work is deemed positive, it signifies that energy is being imparted to the object, resulting in an increase in its energy level. This concept is fundamental to understanding how external forces affect the energy state of a system in the context of the Work-Energy Theorem.

32. Is the Work-Energy Theorem Always Positive?

No, the work done on an object can be both positive and negative, depending on the circumstances. Positive work occurs when energy is transferred to the object, such as when lifting a weight against gravity. Conversely, negative work occurs when the object does work on its surroundings, as seen in situations involving frictional forces. The sign of the work reflects the direction of energy transfer, which can be either into or out of the object.

33. Can the Work-Energy Theorem Be Negative?

Yes, work done can indeed be negative as it represents the transfer of energy from the object to its surroundings. For instance, when an external force, like friction, acts on a moving object and opposes its motion, it does negative work by extracting energy from the object. This negative work results in a decrease in the object’s kinetic energy, illustrating that work can be both positive and negative, depending on the direction of energy flow.

34. What is the underlying rationale for the Work-Energy Theorem in physics?

The Work-Energy Theorem is grounded in the principle of the conservation of energy in physics. It serves as a valuable tool for comprehending how energy is transferred and transformed within a system when external forces are applied. This theorem sheds light on the dynamic interplay between work and energy alterations, allowing for a deeper understanding of physical processes.

35. Can Work Done Be Zero?

Yes, work done can indeed be zero under specific circumstances. This happens when there is either no displacement of an object or when the force applied to the object is entirely perpendicular to the direction of its motion. In both of these scenarios, no change in energy occurs as a result of the work done.

36. Is Work a Vector or Scalar?

Work is classified as a scalar quantity in physics. This categorization implies that work possesses magnitude but does not carry any direction information. Unlike vectors, which have both magnitude and direction (such as velocity or force), work only deals with the amount of energy transferred or transformed.

37. What Is Zero Work?

Zero work, in the context of physics, arises when the force applied to an object exhibits either no component aligned with the direction of the object’s motion or when there is no motion happening at all. In the first case, if the force and the motion are perpendicular, they do not contribute to any work as there is no displacement along the force direction. In the second case, where there’s no motion, the displacement is zero, resulting in zero work done.

38. What Is the Conclusion of the Work-Energy Theorem?

The Work-Energy Theorem is a fundamental principle in physics that establishes a crucial relationship between work done on an object and its change in kinetic energy. According to this theorem, the net work done on an object is equal to the change in its kinetic energy. In essence, it quantifies how energy is transferred or transformed in physical systems. This theorem provides a deep insight into the connection between work and the resulting motion or energy changes in an object, making it a cornerstone concept in the study of mechanics and energy transformations.

39. What Is the Work-Energy Theorem, and How Is It Derived?

The Work-Energy Theorem is a fundamental concept in physics that relates the work done on an object to the change in its kinetic energy. While it doesn’t have a formal proof in the traditional sense, it is derived from the foundational principles of classical mechanics and the definition of work itself. Essentially, it emerges as a result of the integration of force along a path, showing the transformation of energy from work.

40. Who Contributed to the Development of the Work-Energy Theorem?

The Work-Energy Theorem wasn’t discovered by a single individual but rather evolved over time as part of the broader field of classical mechanics. Several prominent scientists made significant contributions to its development. Among them, Galileo Galilei laid the groundwork for understanding the relationship between motion and energy. Sir Isaac Newton, with his laws of motion, played a crucial role in formulating the principles that underlie the Work-Energy Theorem. Therefore, it is a product of collective scientific inquiry and discovery, with many minds contributing to its elucidation.

41. Can Negative Work Be Done?

Negative work occurs when there is an energy transfer from an object to its surroundings, typically resulting from forces that oppose the motion or act in a direction opposite to that of the applied force. This means that the work done reduces the energy of the object in question.

42. What Is the Work-Energy Theorem in Bernoulli’s Theorem?

In the context of Bernoulli’s Theorem in fluid dynamics, the Work-Energy Theorem serves to explain the principle of energy conservation within a fluid flow system. It establishes a connection between changes in pressure, velocity, and height within the fluid, and the work performed by and on the fluid as it moves through the system. Essentially, it helps us understand how the energy of a fluid is distributed and transformed as it flows.

43. What Is the Formula of Energy?

Yes, the formula for energy varies depending on the type of energy under consideration. For kinetic energy (the energy of motion), the formula is KE=1/2mv^2, where KE represents kinetic energy, m is the mass of the object, and v is its velocity. On the other hand, for potential energy near the Earth’s surface (gravitational potential energy), the formula is PE=mgh, where PE represents potential energy, m is the mass of the object, g is the acceleration due to gravity, and h is the height above a reference point.

44. What Is the Unit for Work?

The unit of measurement for work is the joule (J). One joule is equivalent to the work done when a force of one newton (N) is applied to move an object through a distance of one meter (m). In mathematical terms, 1 J = 1 N·m.

45. Is Work and Energy Equal?

Work and energy are related concepts, but they are not equal. Work refers to the process of transferring energy from one system to another. It involves the application of a force to move an object through a distance, resulting in the transfer of energy. Energy, on the other hand, is a broader concept that represents the capacity or ability of a system to do work. In essence, energy is what allows work to be done.

46. How Is the Work-Energy Theorem Used to Solve Problems in Physics?

The Work-Energy Theorem is a fundamental principle in physics that is used to solve a wide range of problems related to motion and energy transfer. To apply this theorem, one calculates the work done on an object and equates it to the change in either its kinetic or potential energy. By using this relationship, physicists can determine various aspects of the object’s motion and understand how energy is transformed within a system. This approach is particularly useful in analyzing mechanical systems and understanding the underlying principles governing their behavior.

47. Is Work a Vector Quantity?

No, work is not classified as a vector quantity. It differs from vector quantities in that it does not possess the two key attributes usually associated with vectors: magnitude and direction. Instead, work is categorized as a scalar quantity, which means it is defined solely by its magnitude. In the context of physics, work represents the amount of energy transferred or transformed during a physical process. Buy Electronic Components, lC chips, Module Darlington, Capacitor, find chips, diode, Transistors, Sensors, and IGBT at Utsource.

48. Is the Work-Energy Theorem Frame Dependent?

No, the Work-Energy Theorem is not dependent on the chosen reference frame. It stands as a fundamental principle in classical mechanics, maintaining its validity and consistency regardless of the specific reference frame used to analyze a given physical situation. This characteristic makes the theorem a universal tool applicable across various frames of reference, ensuring its reliability and broad utility in physics.

49. Is the Work-Energy Theorem Applicable to Situations Involving Friction?

Yes, the Work-Energy Theorem is indeed applicable in situations involving frictional forces. When dealing with such cases, the theorem accounts for the work performed against the frictional force and considers its impact on the overall energy of the system. This versatility in addressing real-world scenarios involving friction highlights the theorem’s practical utility, demonstrating its effectiveness in describing the dynamics of objects subject to frictional forces.

50. Is the Work-Energy Theorem Valid for Variable Forces?

Absolutely, the Work-Energy Theorem remains valid when dealing with scenarios featuring variable forces. It takes into consideration the cumulative effect of all forces acting on an object as it undergoes displacement or motion. This property makes the theorem a valuable and powerful tool in physics for analyzing the behavior of objects subjected to changing forces throughout their trajectories, ensuring its applicability in a wide range of dynamic situations.